ヒストグラムとは？活用例と作り方を簡単に

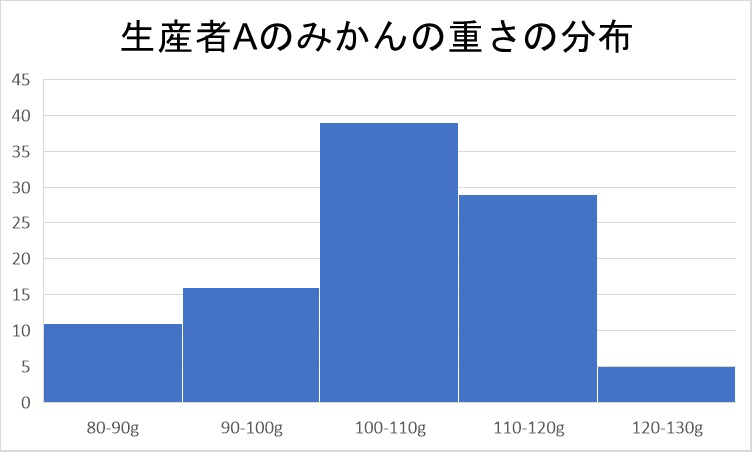
ヒストグラムとは、データの度数分布を視覚的に表現するグラフです。連続的なデータの分布状況を把握しやすいという特徴があり、多くの分野で活用されています。

製造業の品質管理（QC、Quality Control）では「QC七つ道具」の一つとして重要視されています。また、マーケティングにおける「調査結果のプレゼンテーション」や「顧客分析・顧客層の把握」などでも広く利用されています。

ヒストグラムは一見すると棒グラフに似ていますが、その用途や適切な使用場面は異なります。両者の特徴や違いを理解することで、状況に応じて適切なグラフを選択し、効果的なデータ表現が可能となります。

本記事では、ヒストグラムの具体的な活用例や棒グラフとの違い、そしてヒストグラムを簡単に作成する方法について詳しく解説します。データ分析や情報可視化に興味がある方、より効果的なデータ表現を目指す方にとって、有用な情報となるでしょう。

関連記事
・インフォグラフィックとは！作り方と作成する上でのコツを解説！
・ピボットテーブルの使い方とは？基本を解説
・標準偏差とは？求め方やデータ活用法を解説

ヒストグラムとは

ヒストグラムとは、データの度数分布を視覚的に表現するグラフの一種です。このグラフを用いることで、データのばらつきや全体的な傾向を容易に把握することができます。ヒストグラムは、製造現場における品質管理（QC、Quality Control）において頻繁に使用され、「QC七つ道具のひとつ」として広く知られています。さらに、「調査結果のプレゼンテーション」や「顧客分析・顧客層の把握」など、様々な分野で活用されています。

ヒストグラムは一見すると棒グラフに似ていますが、その用途や適切な使用シーンは異なります。両者の特徴と違いを理解することで、状況に応じて適切なグラフを選択し、効果的にデータを表現することが可能となります。

本記事では、ヒストグラムの具体的な活用例や棒グラフとの相違点、そしてヒストグラムを作成する際の基本的な手順についても詳しく解説していきます。これらの情報を通じて、ヒストグラムの有用性と実践的な活用方法について理解を深めることができるでしょう。

ヒストグラムとは

ヒストグラムとは、データの度数分布を視覚的に表現するグラフの一種です。データのばらつきや傾向を効果的に把握できる特徴があります。

具体的には、データを複数の階級（区間）に分類し、それぞれの階級に含まれるデータの数（度数）を縦軸に、階級を横軸に表示します。これにより、データの分布状況を直感的に理解することが可能となります。

ヒストグラムは、製造現場での品質管理（QC、Quality Control）において重要なツールとして用いられており、「QC七つ道具のひとつ」として知られています。また、調査結果のプレゼンテーションや顧客分析・顧客層の把握など、幅広い分野で活用されています。

一見すると棒グラフに似ていますが、ヒストグラムと棒グラフには明確な違いがあります。両者の特徴を理解し、適切に使い分けることが重要です。例えば、ヒストグラムは連続したデータの分布を表現するのに適していますが、棒グラフは個別の項目を比較する際に適しています。

ヒストグラムを活用することで、データの中心傾向や散らばり具合、異常値の有無などを効率的に分析することができます。これにより、データに基づいた意思決定や改善策の立案が可能となり、ビジネスや研究などさまざまな場面で有用なツールとなっています。

ヒストグラムと棒グラフには、以下のような違いがあります。

ヒストグラム	・連続したデータの度数分布を示す ・横軸の階級に連続性がある ・横軸の階級の順番は変えられない（区切り幅は変えられる） ・棒と棒がくっついている
棒グラフ	・1本の棒が示す内容は、それぞれ独立している ・横軸の順番は入れ替え可能 ・棒と棒の間に隙間がある

例えば、ある生産者が生産したみかんの重量の度数分布を示したいときにはヒストグラムが適しています。

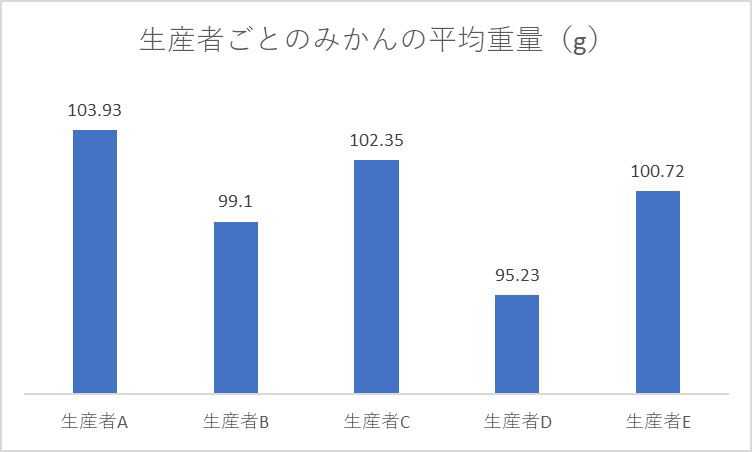
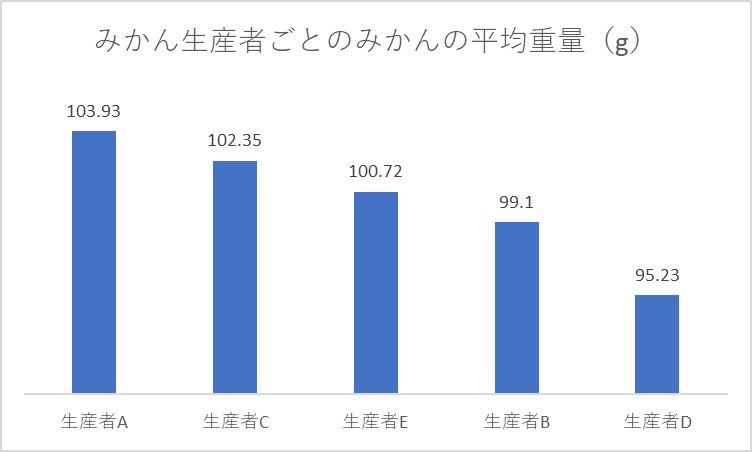
一方生産者A～Eそれぞれが栽培したみかんの平均重量を比べたいときには、棒グラフが適しています。

生産者ごとの平均重量を比べる際には、横軸の順番を入れ替えても問題ありません。

ヒストグラムの種類

ヒストグラムの形には、いくつかの種類（分類）があります。データの分布状況によって、ヒストグラムの形状は変化し、それぞれ特徴的な名称が付けられています。これらの形状を理解することで、データの特性や傾向をより深く把握することができます。ヒストグラムの主な種類には、一般型（左右対称型）、ふた山型、歯抜け型（くし歯型）、右すそ引き型（左すそ引き型）、絶壁型、離れ小島型などがあります。それぞれの形状は、データの特性や分布の偏りを反映しており、分析の際に重要な情報を提供します。

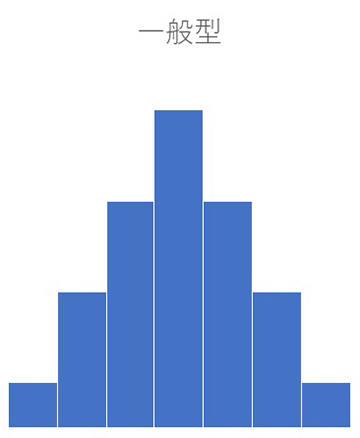
一般型（左右対称型）

一般型（左右対象型）は、ヒストグラムの基本的な形で、中心部の数値が多く、左右対称に広がります。テストの点数分布や身長の分布でよく見られる形です。

左右の広がりがなだらかな場合はばらつきが大きく、鋭い山型になっている場合はばらつきが小さいことがわかります。

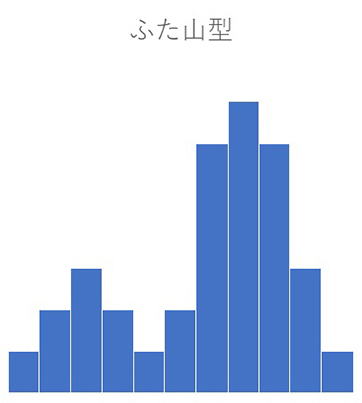
ふた山型

ふた山型（二つ山型）は、中心付近の数値が少なく、左右の数値が多くなっている形です。

このパターンが現れる理由としては、主に以下の3つが考えられます。

・データが2つの異なるグループに分かれている
・中央の値に誤りがある
・異常値が混入している

データが2つのグループに分かれている具体例としては、以下のようなケースが挙げられます。

・男性と女性の身長データが混在している場合
・ベテラン従業員と新人従業員の作業スピードデータが混ざっている場合
・異なる製造ラインや工場で生産された製品の品質データが混合している場合

また、季節性のある商品のデータ分析でも、ふた山型のヒストグラムが現れることがあります。例えば、チョコレートのような商品では、バレンタインデーがある2月の売上が他の月と比べて突出して高くなります。このような場合、2月とそれ以外の月のデータを分けて分析する必要があります。

ふた山型のヒストグラムが現れた場合、データの背景や収集方法を再確認し、必要に応じてデータを分割して別々に分析することが重要です。これにより、より正確な傾向や特徴を把握することができます。

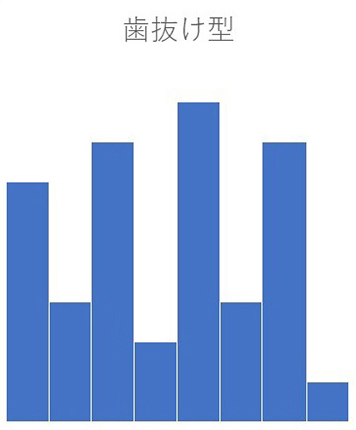
歯抜け型（くし歯型）

歯抜け型になる理由としては、「データが少ない」「区間の幅が狭い」などが考えられます。特に、サンプル数が不十分な場合や、データの区分けが細かすぎる場合に発生しやすい傾向があります。

歯抜け型になってしまった場合は、区間の幅を調整して左右対称型に近づけます。具体的には、区間幅を広げたり、データ数を増やしたりすることで、より滑らかな分布を得ることができます。これにより、データの全体的な傾向をより正確に把握することが可能となります。

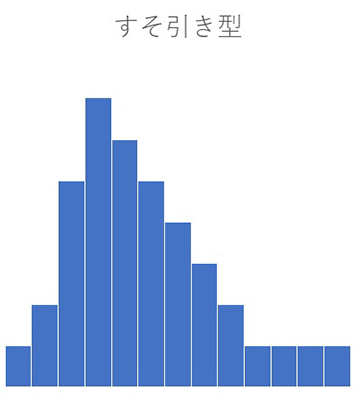
右すそ引き型（左すそ引き型）

右すそ引き型は、頂点が一般型（左右対称型）の左に寄っていて、右に長く裾を引いている形になります。一方左すそ引き型は、データが右に偏っていて、左側に長く裾を引く形です。このような分布は、データに偏りがある場合に見られます。例えば、所得分布などでよく観察される形状です。右すそ引き型の場合、少数の高所得者が存在することで、グラフの右側に長い裾が生じます。一方、左すそ引き型は、データの下限値に近い値が多く、上限値に近づくにつれてデータが少なくなる場合に現れます。

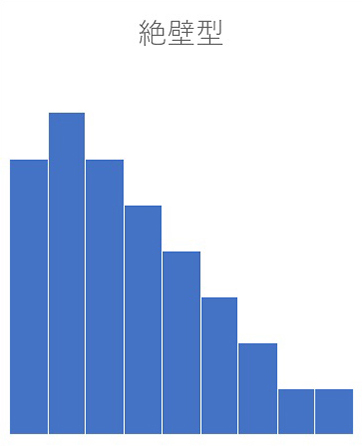
絶壁型

データの頂点が、左右どちらかに極端に寄っている形です。データの数値に上限や下限を設けて、上限・下限を超えた数値を切り捨てている際に現れます。

絶壁型になるのは、集計前に不良品を選別し、不良品なしで分析した場合などです。このような形状のヒストグラムは、データの分布が一方に偏っていることを示しており、製品の品質管理や工程の改善が必要な可能性を示唆しています。

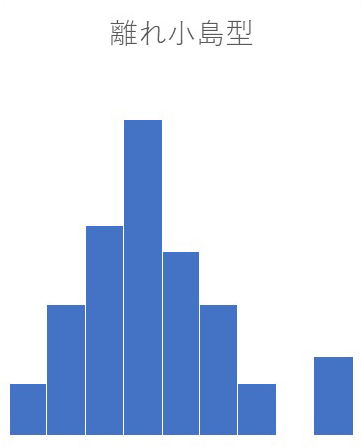
離れ小島型

離れ小島型のヒストグラムでは、中央値とは離れた場所に、少量のデータが存在します。離れ小島（外れ値）が発生することで、平均値が引き下げられたり引き上げられたりします。

離れ小島が発生する理由としては、「集計や入力のミス」「不良品の発生」などが考えられます。このような外れ値の存在は、データ分析において重要な示唆を与える可能性があります。例えば、製造プロセスにおける異常や、特殊な条件下での製品性能などを示唆する場合があります。

離れ小島型のヒストグラムを適切に解釈するためには、外れ値の原因を慎重に調査し、それらのデータポイントが有意義な情報を含んでいるかどうかを判断する必要があります。場合によっては、外れ値を除外して再分析を行うことで、より正確なデータの傾向を把握できることもあります。

ヒストグラムの活用例

ヒストグラムは様々な分野で幅広く活用されています。データの分布や傾向を視覚的に把握できるため、意思決定や分析に役立つ強力なツールとなっています。主な活用例としては、マーケティング、営業、品質管理、教育などの分野が挙げられます。これらの分野では、ヒストグラムを用いることで、消費者行動の把握、顧客分析、製品品質の管理、学習成果の評価など、多岐にわたる目的に応じたデータの可視化と分析が可能となります。ヒストグラムを効果的に活用することで、各分野における課題の発見や改善策の立案に繋げることができます。

マーケティング

ヒストグラムはマーケティングの分野で、「消費者の行動」や「市場調査の結果」を示すときに使われることが多い傾向にあります。

ターゲット層の行動や傾向を効率的に把握・理解したり、「地域ごと」「性別ごと」「年齢ごと」で簡単に比較したりできるためです。把握したターゲット層の特徴を、より効果的なマーケティング戦略の立案に生かすことが可能となります。把握したターゲット層の特徴を、より効果的なマーケティング戦略の立案に活かすことが可能となります。

また売上データをヒストグラムで視覚化することで、人気商品の価格帯がわかるなど、販売戦略の改善にも繋がります。

関連記事
・データドリブンとは？データドリブンマーケティング実現のために必要なことを解説
・データサイエンスとは！意味や概念をわかりやすく解説！

営業

ヒストグラムは営業活動にも使えます。

例えば顧客の購入頻度や累計購入金額に応じてアプローチを変えたいときに、「購入頻度」「累計購入金額」「最終購入日から何日経っているか」のヒストグラムをつくることで、顧客を「潜在顧客」「初回購入のみの顧客」「リピーター」といったグループ分けの参考になります。

「ある商品が売れる時期」「あまり売れない時期」や、エリア・店舗ごとの売り上げにおける特徴を把握することも可能です。

ヒストグラムを2つ重ねれば、「営業活動の改善をしたあと、売上がどう変わったか」も一目で把握できます。

関連記事
・リピーターとは！ 増やすための施策、獲得の重要性を解説！
・インサイトセリング、ビジョンセリングとは？マーケターが知っておきたい新たな営業手法

品質管理

ヒストグラムは製造現場における品質管理でも使われてきました。

例えば製造された「部品の重さやサイズ」「製造にかかる時間」のデータをヒストグラムにしたとき、何らかの異常値がある場合には、「製造過程に問題がある」と推測できます。

データを分析する視点によって、「どの製造グループ・スタッフ」「どの時間帯」「どの機械」で問題が発生しているのかもわかり、対策しやすくなります。

教育

教育分野でもヒストグラムが活用されています。

例えば「テストの成績分布」をヒストグラムで示すことが良くあります。テストを作成した教員が想定した点数の範囲内に人数が集まっているかどうか見ることで、「テストの難易度」
「授業の内容や指導方法」を見直すきっかけになるでしょう。

また、ヒストグラムは学習者自身の理解度や進捗を可視化するツールとしても有効です。例えば、定期的に実施される模擬試験の結果をヒストグラムで表すことで、自身の成績の推移や全体の中での位置づけを把握しやすくなります。これにより、学習者のモチベーション向上や、効果的な学習計画の立案にも役立ちます。

ヒストグラムの特長

ヒストグラムは、データの分布や傾向を視覚的に表現するグラフとして広く活用されています。その特長として、以下の3つが挙げられます。まず、データの分布を直感的に把握できることです。棒の高さや形状から、データの集中度や散らばり具合を一目で理解することができます。次に、階級分けによるデータの整理が可能な点です。連続的なデータを適切な区間に分類することで、全体の傾向をつかみやすくなります。最後に、グラフの形状からデータの特徴を読み取れることです。左右対称型や右すそ引き型など、ヒストグラムの形状によってデータの性質や偏りを判断することができます。これらの特長により、ヒストグラムは様々な分野でデータ分析や意思決定の支援ツールとして重宝されています。

データの分布が視覚的にわかる

データの分布が視覚的にわかるのは、ヒストグラムがもつ特長のひとつです。ヒストグラムなら、一目でデータのばらつきを把握できます。これにより、データの全体的な傾向や特徴を素早く理解することが可能となります。

また離れ小島型の発生などきれいなヒストグラムにならない場合は、異常なデータや、間違ったデータの混入があったと判断できます。このような異常値の発見は、データ分析において非常に重要な役割を果たします。

視覚的に把握できることで、「地域ごとの比較」「事業所ごとの比較」などもしやすくなりますし、プレゼンや説明の資料としても有効です。ヒストグラムを二つ重ねることで、「施策導入前後の比較」などもしやすくなります。

このように、ヒストグラムは複雑なデータを視覚化することで、直感的な理解を促進し、効果的なデータ分析や意思決定をサポートする強力なツールとなります。

階級分けによるデータの整理ができる

階級分けによってデータを整理できるのも、ヒストグラムの特長です。ヒストグラムは、収集されたデータを適切な階級に分類することで、その分布や傾向を効果的に可視化するグラフです。この階級分けにより、大量のデータを整理し、意味のある情報として分析することが可能になります。

階級の設定は自由に決められますが、データの特性や分析の目的に応じて、最適な分け方を選択することが重要です。適切な階級分けを行うことで、データの中に潜む傾向や特徴を浮き彫りにし、より深い洞察を得ることができます。例えば、顧客の年齢分布や製品の品質データなど、様々な場面でこの特長を活かすことができます。

データの特長を形状で読み取れる

データの特長をグラフの形から読み取れるのも、ヒストグラムの特長です。ヒストグラムではデータの分布が直感的にわかり、さらに分布の特徴（上限や下限がどこなのか、どこに偏っているのかなど）もわかります。

例えば、ある企業の従業員たちの年齢分布をヒストグラムで示すと、その企業の傾向が読み取れます。若手社員が多い右すそ引き型なのか、ベテラン社員が多い左すそ引き型なのか、あるいは中堅社員が中心の一般型なのかが一目瞭然となります。また、ふた山型であれば新卒採用と中途採用の二極化が進んでいる可能性も示唆されます。

このように、ヒストグラムは全体の大まかな傾向を把握したいときに非常に役立つツールです。データの特徴を視覚的に捉えることで、より深い分析や戦略立案のきっかけを得ることができます。

ヒストグラムの作成方法

ヒストグラムの作成方法について、具体的な手順を解説します。ヒストグラムを正確に作成することで、データの分布や傾向を視覚的に把握しやすくなります。以下の手順に従って、効果的なヒストグラムを作成しましょう。

まず、ヒストグラム作成の目的を明確にすることが重要です。次に、十分な量のデータを収集し、整理します。一般的に100以上のデータ数が望ましいとされています。

データが揃ったら、度数分布表を作成します。度数分布表は、ヒストグラム作成の基礎となる重要な要素です。区間の数や幅、境界値などを適切に設定することで、より正確なヒストグラムを作成できます。

度数分布表が完成したら、各区間のデータ数をカウントします。このステップでは、正確さが求められます。カウントミスがあると、ヒストグラムの形状に影響を与えてしまうため、注意が必要です。

最後に、横軸に区間（階級）、縦軸にデータの数（度数）を設定し、実際にヒストグラムを作図します。この際、グラフの見やすさにも配慮しましょう。

これらの手順を丁寧に踏むことで、信頼性の高いヒストグラムを作成することができます。ヒストグラムを通じて、データの特徴や傾向を効果的に分析し、意思決定や改善活動に活用しましょう。

作成目的を明確にする

ヒストグラムを作成する際、まず重要なのは作成目的を明確にすることです。調査目的が不明確だと、どのようなデータを収集すべきかわからなくなってしまいます。そのため、ヒストグラム作成の第一歩として、目的を明確に定義することが重要です。

ヒストグラムの作成目的には様々なものがあります。例えば、「生徒の成績を把握し、改善が必要な教科・科目を特定したい」「営業成績の分布を分析し、効果的な指導方法を見出したい」「製造工程における不具合の要因を特定し、品質改善につなげたい」などが挙げられます。

目的を明確にすることで、必要なデータの種類や範囲、収集方法が明らかになります。また、ヒストグラムを作成した後の分析や意思決定にも大きく影響するため、この段階で十分な検討を行うことが望ましいでしょう。

データを収集し整理する

ヒストグラムの元になるデータを収集します。一般的にデータ数は、100程度以上必要だと言われています。データを収集したら、最大値と最小値を求めておきましょう。ヒストグラムを作成する際は、データの特性や分布を適切に表現できるよう、十分な量のデータを集めることが重要です。また、収集したデータの中に異常値や外れ値がないか確認し、必要に応じて除外や調整を行うことも検討しましょう。データの整理段階で、全体の傾向を把握しておくことで、後の分析や解釈がスムーズになります。

度数分布表を作成する

ヒストグラムを作成する前には、度数分布表を作成します。

度数分布表の作成に必要なのは以下の要素です。

要素	決め方の目安・方法
区間の数	・通常は「√データ数（データ数の平方根の整数部分）」で計算 ※スタージェスの公式というもので目安を求める方法もある
区間の幅	（データの最大値）-（最小値）/区間の数
下側境界値	第一区間の下側境界値＝（最小値）-（測定単位/2）
上側境界値	（下側境界値）＋（区間の幅）
区間の中心値	｛（下側境界値）＋（上側境界値）｝/2

ある製品のサイズを計測したデータを想定した場合の、度数分布表のイメージは以下の通りです。データ数は100で、測定単位（測定の刻み）は0.01、最小値49.50、最大値50.56です。

No.	区間	区間の中心値	度数（データの数）
1	49.495～49.605	49.550
2	49.605～49.715	49.660
3	49.715～49.825	49.770
4	49.825～49.935	49.880
5	49.935～50.045	49.990
6	50.045～50.115	90.100
7	50.115～50.265	90.210
8	50.265～50.375	90.320
9	50.375～50.485	90.430
10	50.485～50.595	90.540
計

データの度数をカウントする

データの数をカウントして、度数分布表に記入します。

度数の記入が終わった度数分布表のイメージは以下の通りです。

No.	区間	区間の中心値	度数（データの数）
1	49.495～49.605	49.550	5
2	49.605～49.715	49.660	4
3	49.715～49.825	49.770	7
4	49.825～49.935	49.880	11
5	49.935～50.045	49.990	12
6	50.045～50.115	90.100	23
7	50.115～50.265	90.210	13
8	50.265～50.375	90.320	13
9	50.375～50.485	90.430	7
10	50.485～50.595	90.540	5
計			100

「横軸」と「縦軸」を設定する

横軸には区間（階級）を記入します。そして縦軸にはデータの数（度数）を書き入れます。これで実際にヒストグラムを作図する準備が整いました。

度数分布表をもとに、各区間の度数に応じた柱を書き入れて完成です。

横軸の設定では、各区間の境界値を明確に示すことが重要です。縦軸の設定では、データの最大度数を考慮して適切な目盛りを決定します。これにより、データの分布が視覚的に理解しやすくなります。

ヒストグラムを作図する

上記は手書きでヒストグラムを作図する方法ですが、Microsoft Excelを使えば、簡単にヒストグラムを作成できます。

Microsoft Excelでヒストグラムを作図する方法は以下の通りです。

1. データを準備する
2. データを選択肢、「挿入タブ＞統計データの挿入＞ヒストグラム」をクリック
3. グラフにタイトルを追加
4. 横軸付近で右クリックし、軸の書式設定でビンの幅を調整
5. 指定数値より大きい数・小さい数をまとめたい場合は「ビンのオーバーフロー」「ビンのアンダーフロー」で設定

Microsoft Excel2016以降からは、度数分布表の作成なしでデータから直接ヒストグラムを作成できるようになっています。なお度数分布表からヒストグラムを作成して横軸の幅がおかしいときには、軸の書式設定でビンを「分類項目別」にしましょう。

ヒストグラム作成時に注意すること

ヒストグラムを作成する時に注意したい点を紹介します。

適切な階級の設定

ヒストグラムを作成する時にもっとも注意したいのは、適正な階級を設定することです。ヒストグラムでは、階級幅のとり方によってグラフの形が変わって印象も変わり、誤った解釈につながりかねません。

例えば階級幅が狭すぎると、きれいな山形の分布にならず歯抜け型になってしまい、データの傾向が掴みにくくなってしまう可能性があります。

また階級の区切り方が中途半端だと、わかりにくくなります。「10ごと」「100ごと」など、きれいな数字で区切るほうがわかりやすいでしょう。また「1以上10未満」など、「以上」と「未満」を明確にすることも重要です。

階級幅の数や決め方に目安はありますが、「必ずこうしなさい」というルールはありません。

ヒストグラムを一目見ればデータの特徴がわかるように区切ることが求められますので、実務では、いくつかグラフを作ってみて分布がわかりやすい幅を採用することが多いです。

まとめ：ヒストグラム活用でわかりやすくデータを提示しよう

ヒストグラムはデータの分布やばらつきを一目で確認できるグラフです。会議資料やプレゼン資料にヒストグラムを活用することで、「数字を使って言いたいこと」を伝えやすくなります。

手書きで作成するのは手間がかかりますが、エクセルを使えば簡単に作成できます。

ただし区間幅の設定によっては分布の傾向がわかりにくくなってしまう可能性があります。上記の場合は区間幅の設定を変更するなどの工夫が必要です。